3.3 模型并行TP
张量并行¶
学习目标¶
- 理解张量并行的底层原理
- 在前面的章节中, 已经学习了流水线并行, 数据并行. 本小节将要介绍最重要, 也是基于Transformer做大模型最基本的并行范式: NVIDIA的张量模型并行(TP). 基本思想就是把模型的参数纵向切开, 放到不同的GPU上进行独立计算, 然后再做聚合.
切分权重的两种方式¶
- 在此先做一些参数假设: 设输入数据为X, 参数为W, X的维度 = (b, s, h), W的维度 = (h, h')
- b: batch_size, 表示批次大小
- s: sequence_length, 表示输入序列的长度
- h: hidden_size, 表示每个token向量的维度
- h': 参数W的hidden_size
- 每次forward的过程如下图所示(为了方便, 图中是b=1的情况):
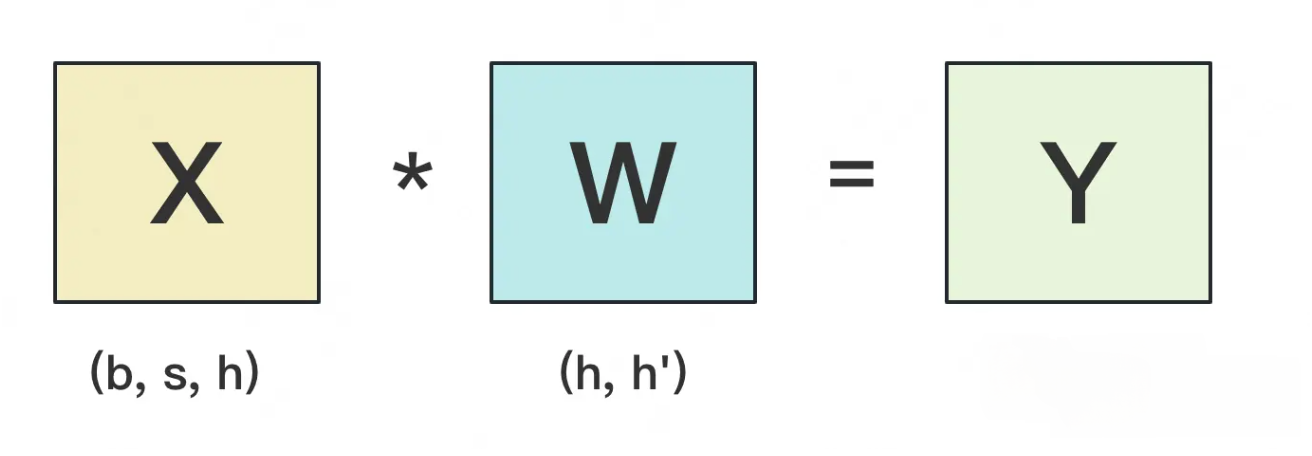
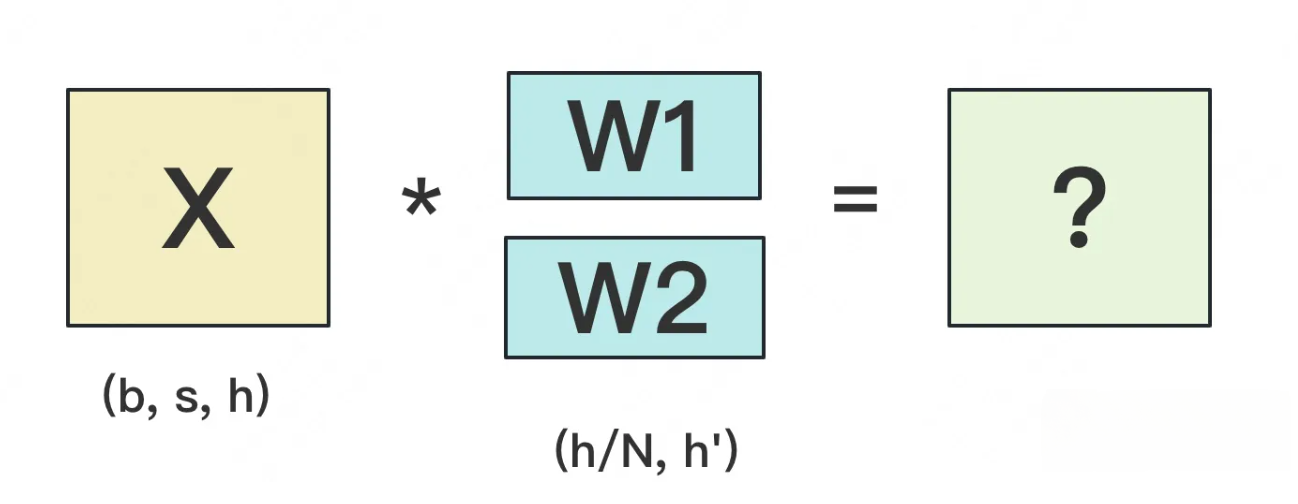
- 假设现在W太大, 导致单卡装不下. 我们需要把W切开放到不同的卡上, 则面临三个主要问题:
- 1: 怎么切分W
- 2: 切完W后, 怎么做forward
- 3: 做完forward后, 怎么做backward, 进而求出梯度, 更新权重
- 一般来说, 我们可以沿着W的行, 或者列切分W. 下面我们分别介绍这两种切割办法, 并说明它们是如何做forward和backward的.
按行切分权重¶
- forward: 我们用N来表示GPU的数量, 有几块GPU, 就把W按行维度切成几份, 下图展示了N=2时的切割方式:
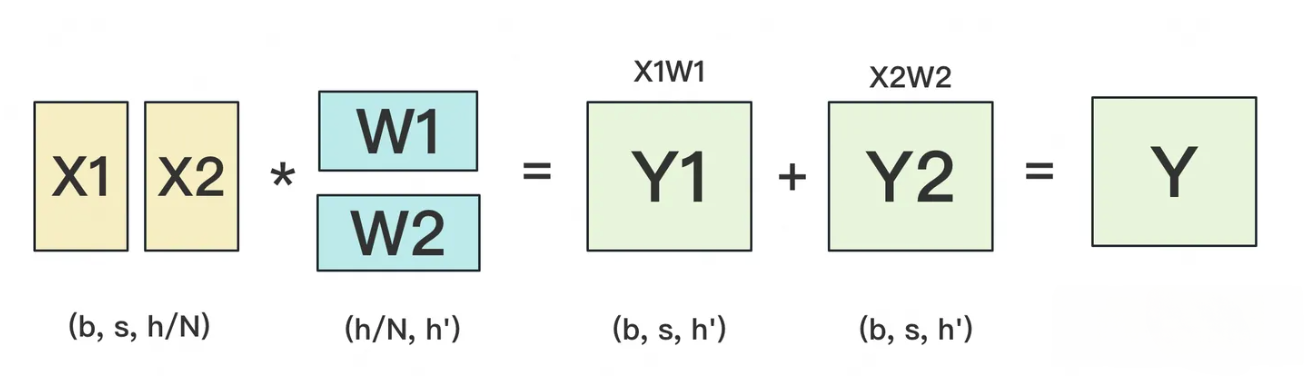
- W按照行维度切开后, X的维度和它不对齐了, 那怎么做矩阵乘法呢? 很简单, 再把X"按列切开"就行了, 如下图所示:
- backward: 做完forward, 取得预测值Y, 进而可计算出损失L, 接下来就能做backward了. 我们重画一下forward的过程, 并在其中加入backward的部分, 整体流程图如下:
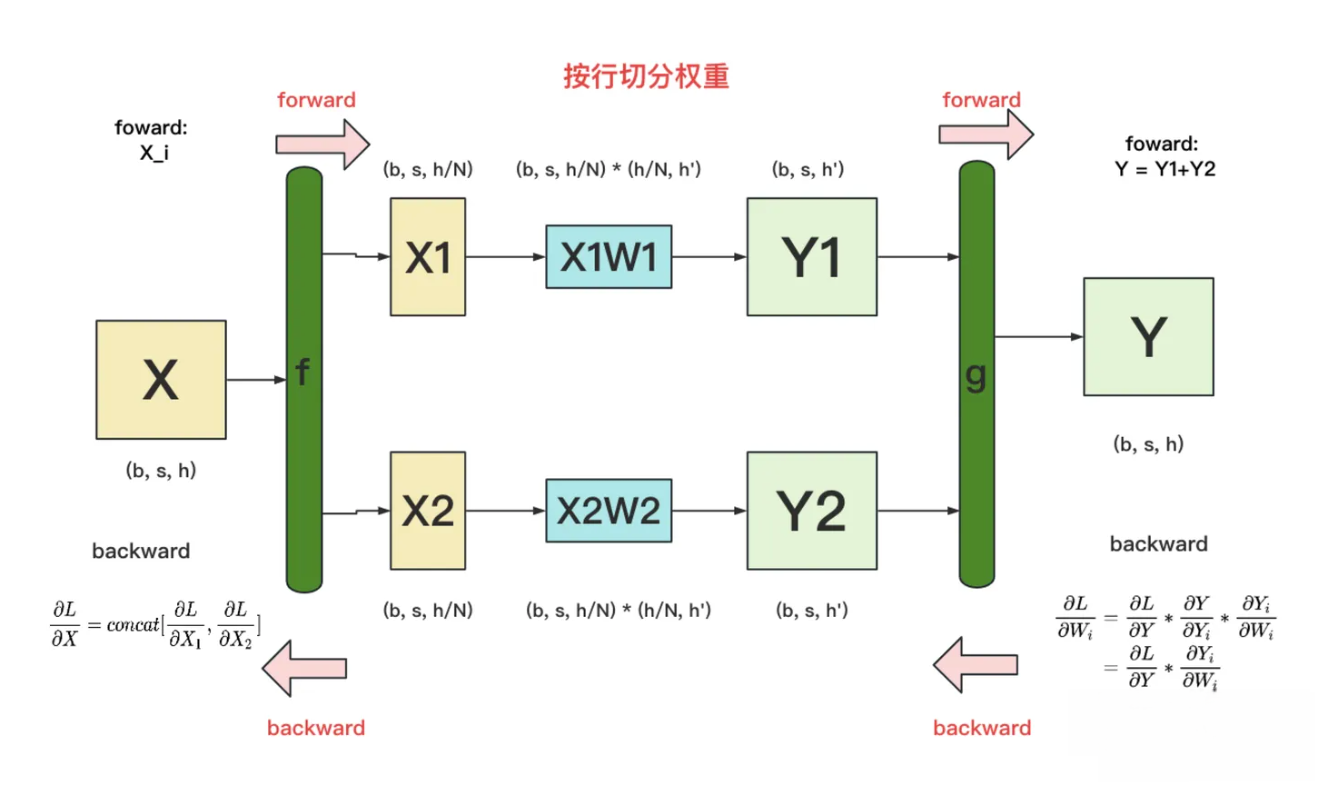
g的backward过程, 要对Wi求梯度, 结果显示只要把最后一层对Y的偏导同时广播到两块GPU上, 两块GPU就可以独立计算各自权重的梯度了.
f的backward过程, 如果模型存在多层时, 梯度要从上一层向下一层传播. 比如梯度要先传播到X, 然后才能往下一层继续传递.
按列切分权重¶
- foward: 按列切分权重后, forward计算图如下图所示:

- backward: 流程如下图所示:
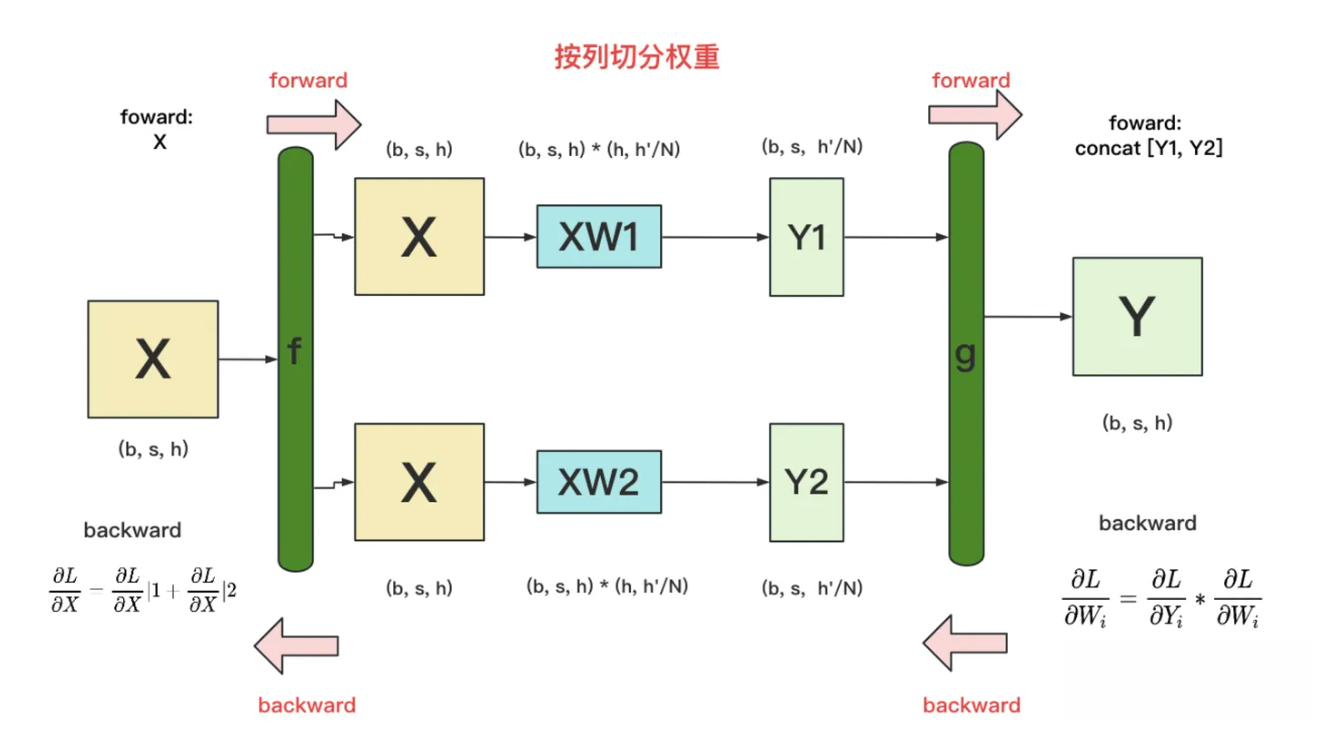
- f的backward, 因为对于损失L, X既参与了XW1的计算, 也参与了XW2的计算, 因此最终的偏导公式中的|1表示第1块GPU上计算到的X的梯度, |2表示第2块GPU上计算到的X的梯度.
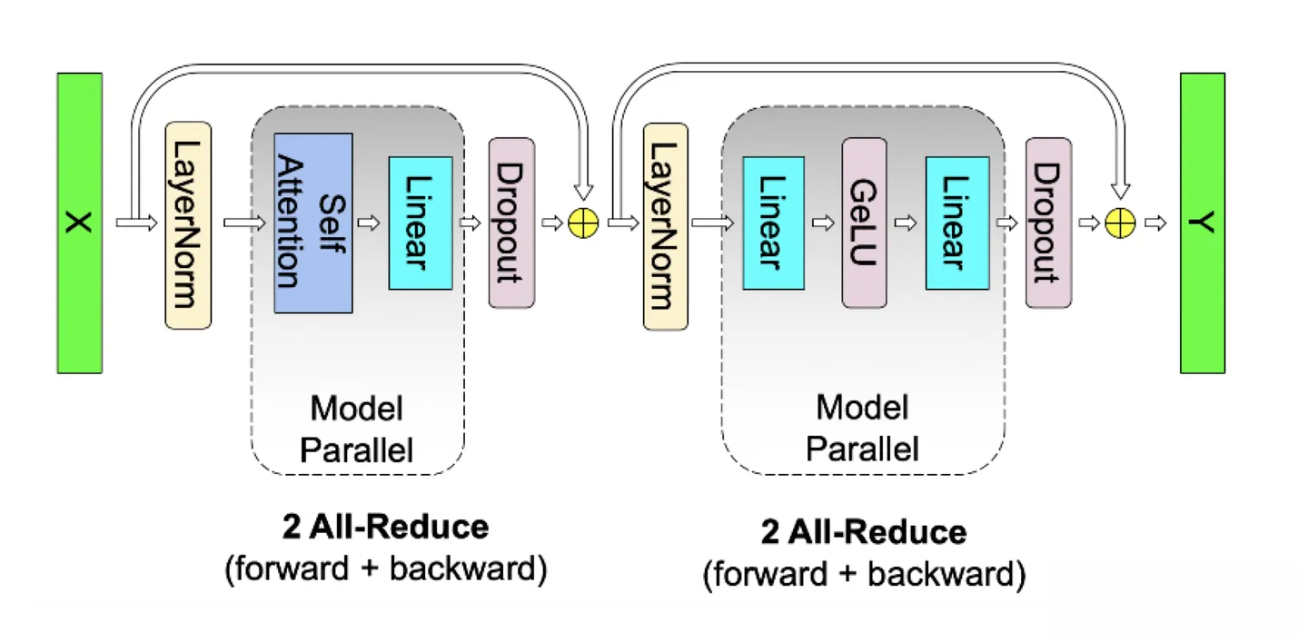
MLP层¶
- MLP层的计算过程如下图所示:
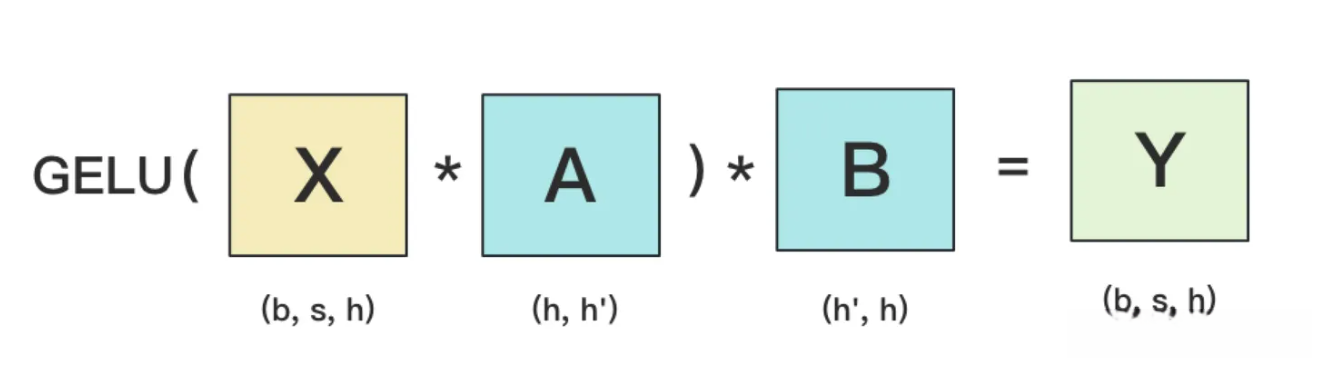
- 其中GELU是激活函数, A和B分别是两个线性层. 假设有N块GPU, 要把MLP层的权重拆分到上面做计算, 方法如下图所示:
- 对A采用列切分
- 对B采用行切分
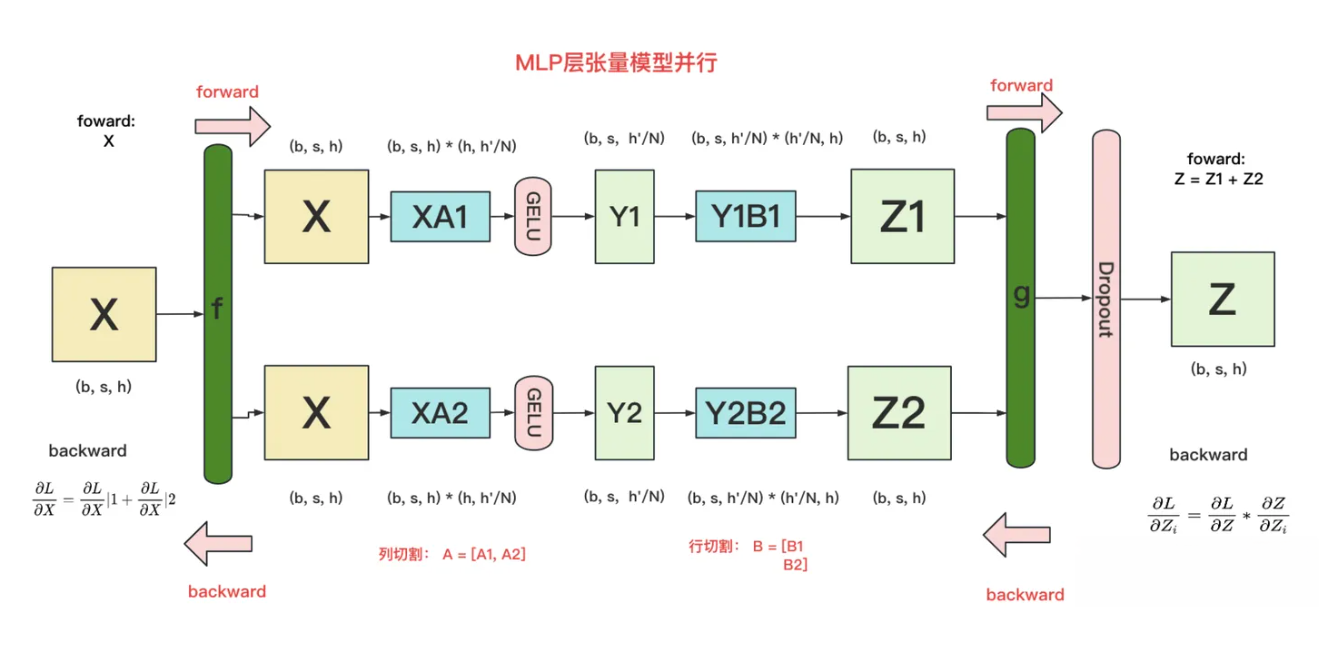
f的forward: 把输入X拷贝到两块GPU上, 每块GPU即可独立做forward计算.
g的forward: 每块GPU上的forward计算完毕, 取得Z1和Z2后, GPU间做一次AllReduce, 相加结果产生Z.
g的backward: 只需要把L对Z的偏导拷贝到两块GPU上, 两块GPU就能各自独立做梯度计算了.
f的backward: 当前层的梯度计算完毕, 需要传递到下一层继续做梯度计算时, 我们需要求得L对X的偏导, 此时两块GPU做一次AllReduce, 把各自的梯度相加即可.
- 为什么我们对A采用列切分, 对B采用行切分呢? 这样设计的原因是, 我们尽量保证各GPU上的计算相互独立, 减少通讯量. 对A来说, 需要做一次GELU的计算, 而GELU函数是非线形的, 它的性质如下:

- 这就意味着: 如果对A采用行切分, 我们必须在做GELU前, 做一次AllReduce, 这样就会产生额外的通讯量. 但是如果对A采用列切分, 那每块GPU就可以继续独立计算了. 一旦确认好A做列切分, 那么也就相应的B就需要做行切分了.
Self-Attention层¶
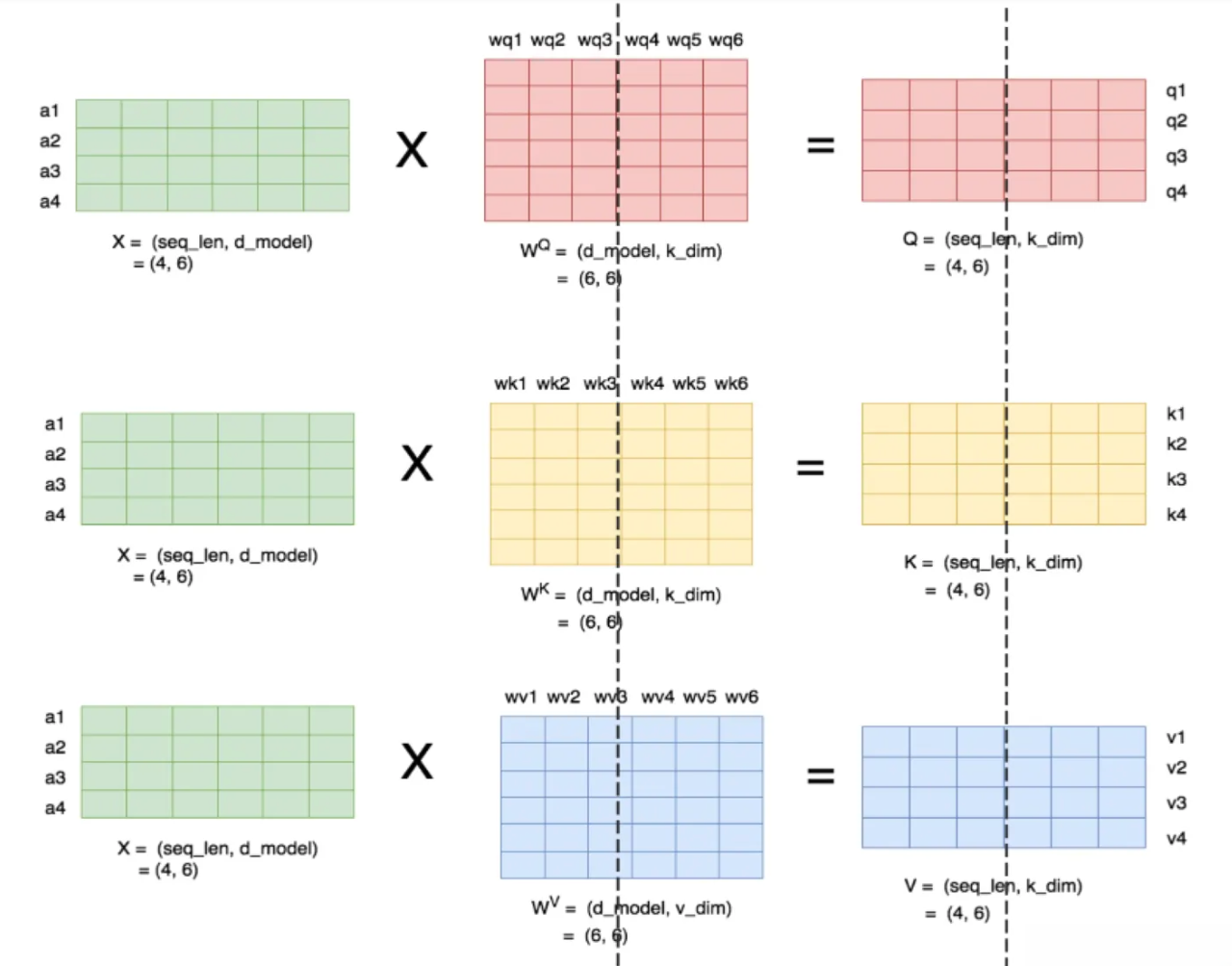
- 下图展示了当num_heads = 2时attention层的计算方法. 即对每一块权重, 我们都沿着列方向(k_dim)维度切割一刀. 此时每个head上的WQ, WK, WV 的维度都变成(d_model, k_dim//2). 每个head上单独做矩阵计算, 最后将计算结果concat起来即可, 整个流程如下:
- 可以发现, attention的多头计算简直是为张量模型并行量身定做的, 因为每个头上都可以独立计算, 最后再将结果concat起来. 也就是说, 可以把每个头的参数放到一块GPU上, 整个过程如下图所示:

- 对三个参数矩阵Q, K, V, 按照"列切分", 每个头放到一块GPU上, 做并行计算. 对线性层B, 按照"行切分", 切分的方式和MLP层基本一致, 其forward与backward原理也一致. 最后, 在实际应用中, 并不一定按照一个head占用一块GPU来切分权重, 我们也可以一个或多个head占用一块GPU, 这依然不会改变单块GPU上独立计算的目的. 所以实际设计时, 我们尽量保证head总数能被GPU个数整除.
- 综上所述, 可以把self-attention层拼接起来看一下整体的计算逻辑:
Embedding层¶
- 关于Embedding的分析, 分成输入层和输出层.
输入层Embedding¶
- Embedding层一般由两个部分组成:
- word embedding: 维度(v, h), 其中v表示词表大小.
- positional embedding: 维度(max_s, h), 其中max_s表示模型允许的最大序列长度.
- 对positional embedding来说, max_s本身不会太长, 因此每个GPU上都拷贝一份, 对显存的压力也不会太大. 但是对word embedding来说, 词表的大小就很可观了, 因此需要把word embedding拆分到各个GPU上, 具体的做法如下:
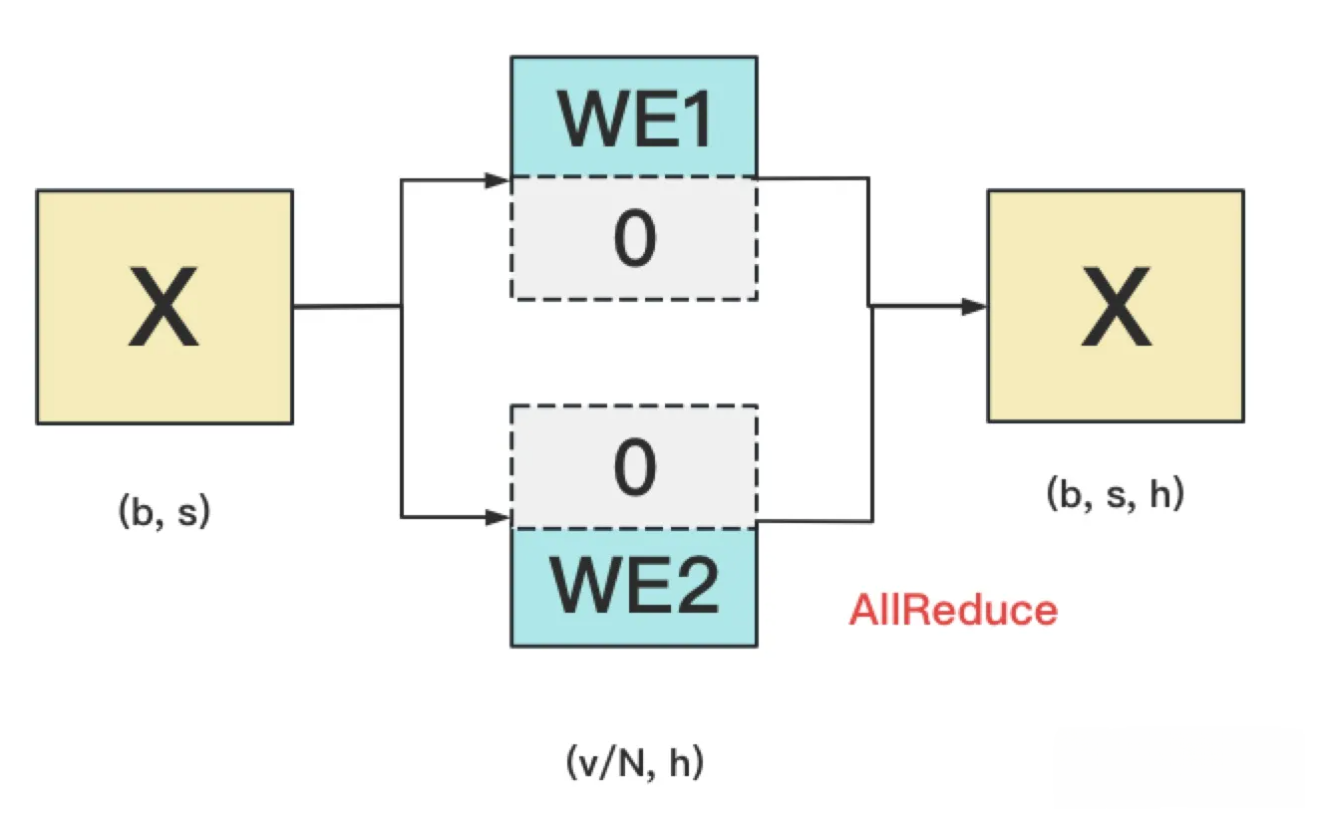
对于输入X, 过word embedding的过程, 就是等于用token的序号去word embedding中查找对应词向量的过程. 例如, 输入数据为[0, 212, 7, 9], 数据中的每一个元素代表词序号, 我们要做的就是去word embedding中的0, 212, 7, 9行去把相应的词向量找出来.
假设词表中有300个词, 现在我们将word embedding拆分到两块GPU上, 第一块GPU维护词表[0, 150), 第二块GPU维护词表[150, 299). 当输入X去GPU上查找时, 能找到的词, 就正常返回词向量, 找到不到就把词向量中的全部全素都置0. 按此方式查找完毕后, 每块GPU上的数据做一次AllReduce, 就能得到最终的输入. 在本例中, 第一块GPU的查找结果为[ok, 0, ok, ok], 第二块为[0, ok, 0, 0], 两个向量一相加, 变为[ok, ok, ok, ok].
输出层Embedding¶
- 输出层中, 同样有一个word embedding, 把输入再映射回词表里, 得到每一个位置的词. 一般来说, 输入层和输出层共用一个word embeding. 其计算过程如下:
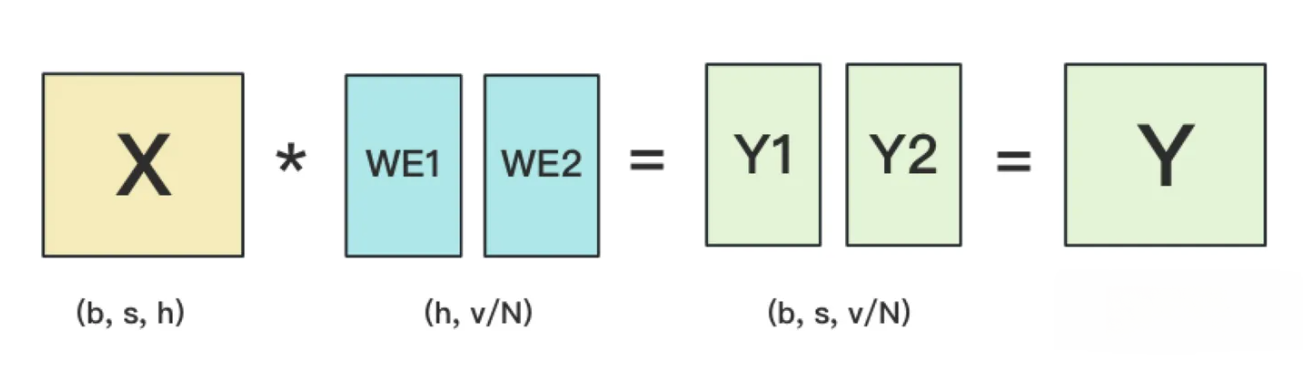
- 注意: 我们必须时刻保证输入层和输出层共用一套word embedding. 而在backward的过程中, 我们在输出层时会对word embedding计算一次梯度, 在输入层中还会对word embedding计算一次梯度. 在用梯度做word embedding权重更新时, 我们必须保证用两次梯度的总和进行更新!!!
- 核心: 当模型的输入层到输入层都在一块GPU上时(即流水线并行深度=1), 我们不必担心这点(实践中大部分用Megatron做并行的项目也是这么做的). 但若模型输入层和输出层在不同的GPU上时, 我们就要保证在权重更新前, 两块GPU上的word embedding梯度做了一次AllReduce!!!
Cross-Entropy层¶
- 具体来看计算损失函数的一层, 输出层过完embedding后的样子如下图所示:
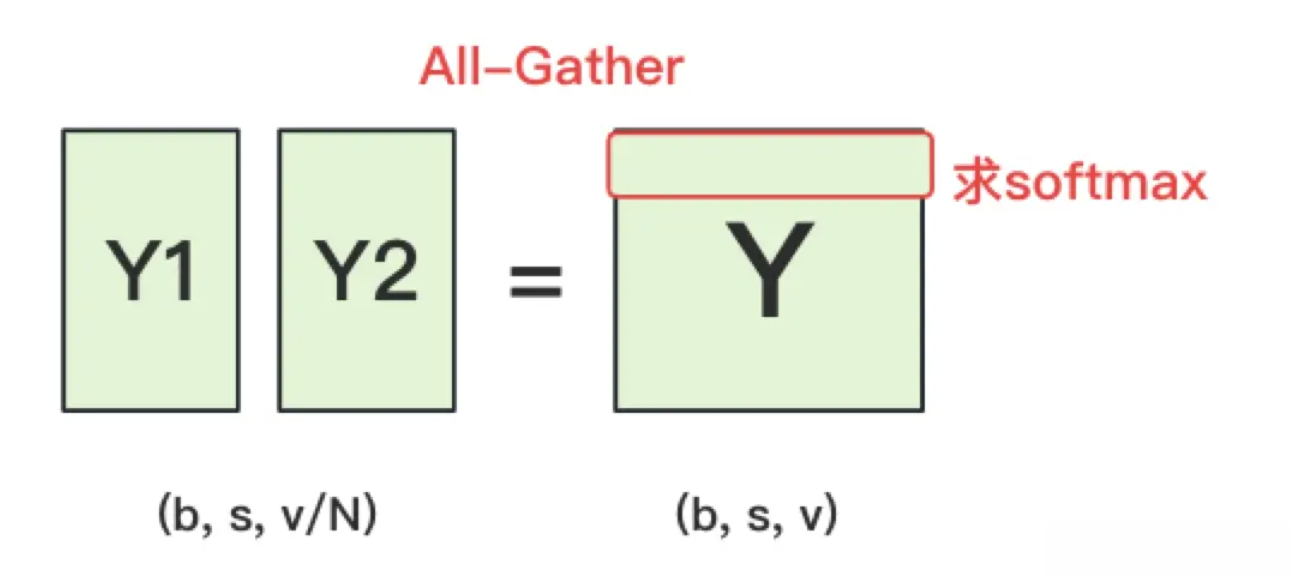
- 正常来说, 我们需要对Y1和Y2做一次All-Gather, 把它们concat起来形成Y, 然后对Y的每一行做softmax, 就可得到对于当前位置来说每个词出现的概率. 接着, 再用此概率和真值组做cross entropy即可.
- 但是All-Gather会产生额外的通讯量b*s*v, 当词表v很大时, 这个通讯开销也不容忽视. 针对这种情况, 可以做如下优化:
- 1: 每块GPU上, 我们可以先按行求和, 得到各自GPU上的GPU_sum(e).
- 2: 将每块GPU上结果做AllReduce, 得到每行最终的sum(e), 也就softmax中的分母, 此时的通讯量为b*s*v.
- 3: 在每块GPU上, 即可计算各自维护部分的e/sum(e), 将其与真值做cross-entropy, 得到每行的loss, 按行加总起来以后得到GPU上的loss.
- 4: 将GPU上的loss做AllReduce, 得到总Loss, 此时通讯量为N.
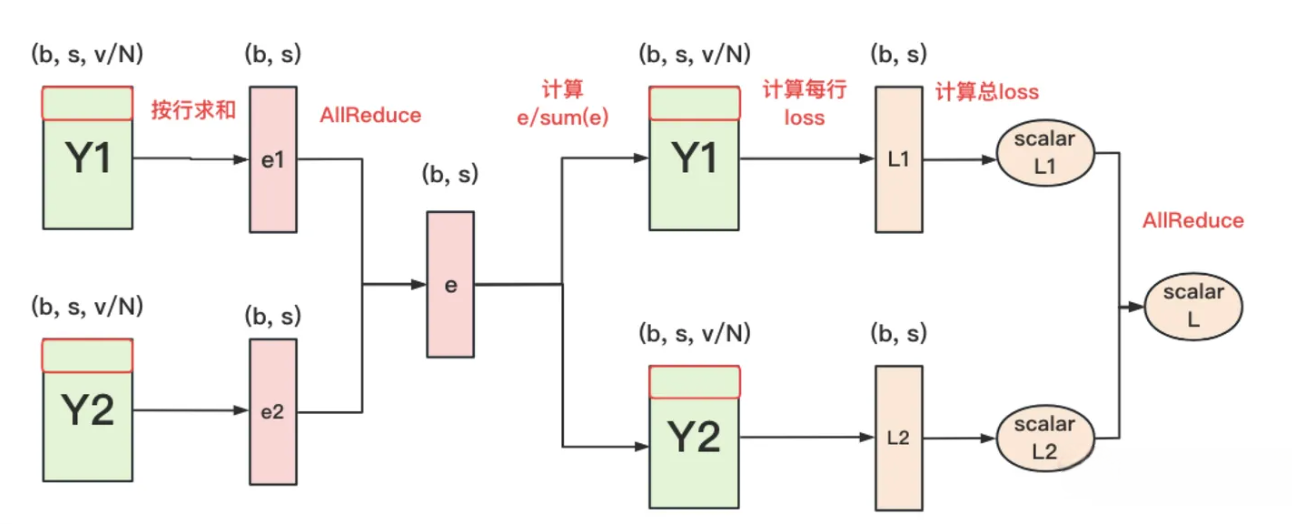
- 总结: 将通信量从最初始的b*s*v, 大大降低到b*s + N.
经典TP+DP模式¶
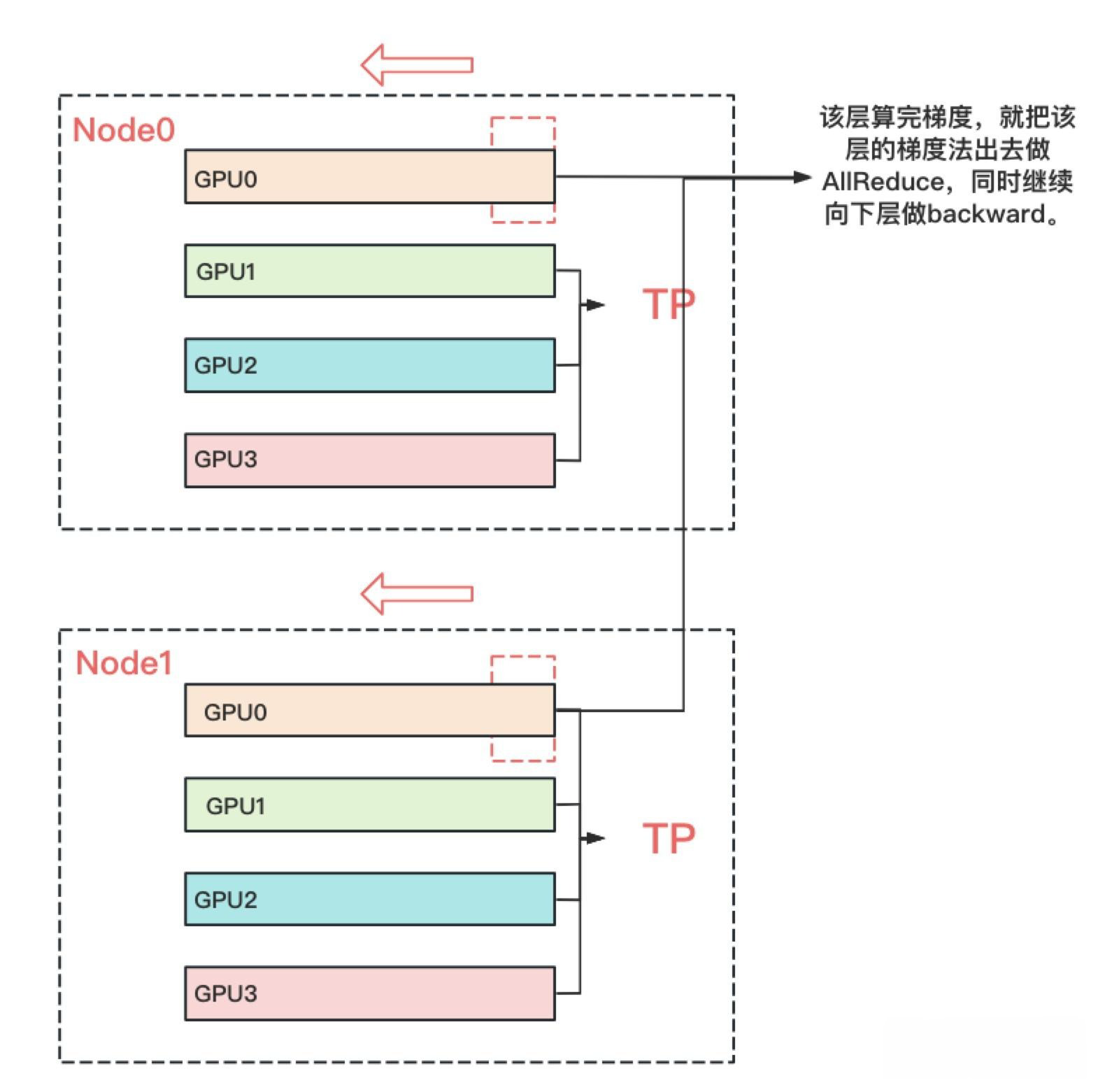
- 到这里为止, 我们基本把张量模型并行的计算架构说完了. 在实际应用中, 对Transformer类的模型, 采用最经典方法是张量模型并行 + 数据并行, 并在数据并行中引入ZeRO做显存优化, 具体的架构如下:
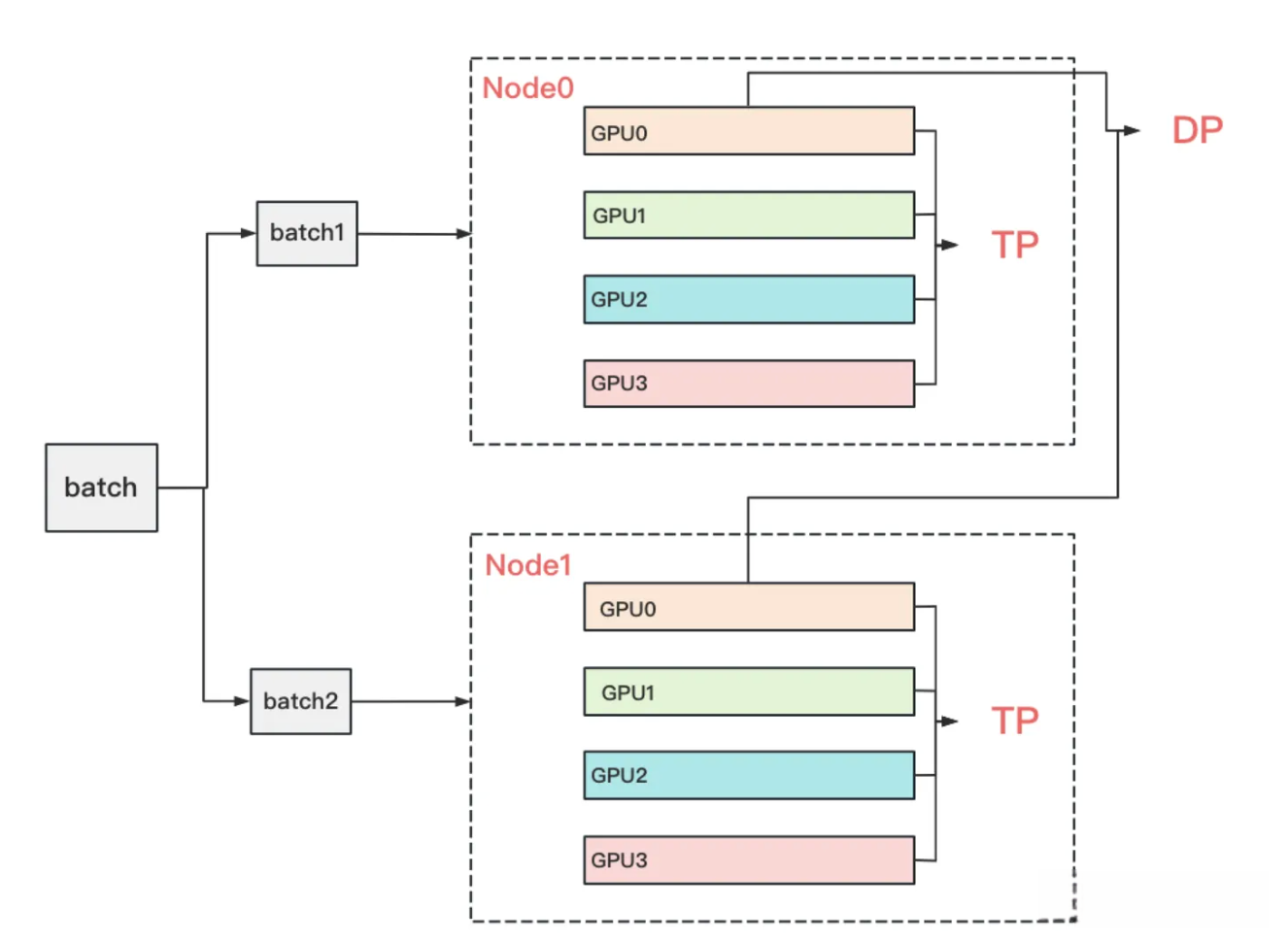
- 其中node表示一台机器, 一般我们在同一台机器的GPU间做张量模型并行. 在不同的机器上做数据并行. 图中颜色相同的部分, 为一个数据并行组. 凭直觉我们可以知道这么设计大概率和两种并行方式的通讯量有关. 具体来说, 它与TP和DP模式下每一层的通讯量有关, 也与TP和DP的backward计算方式有关.
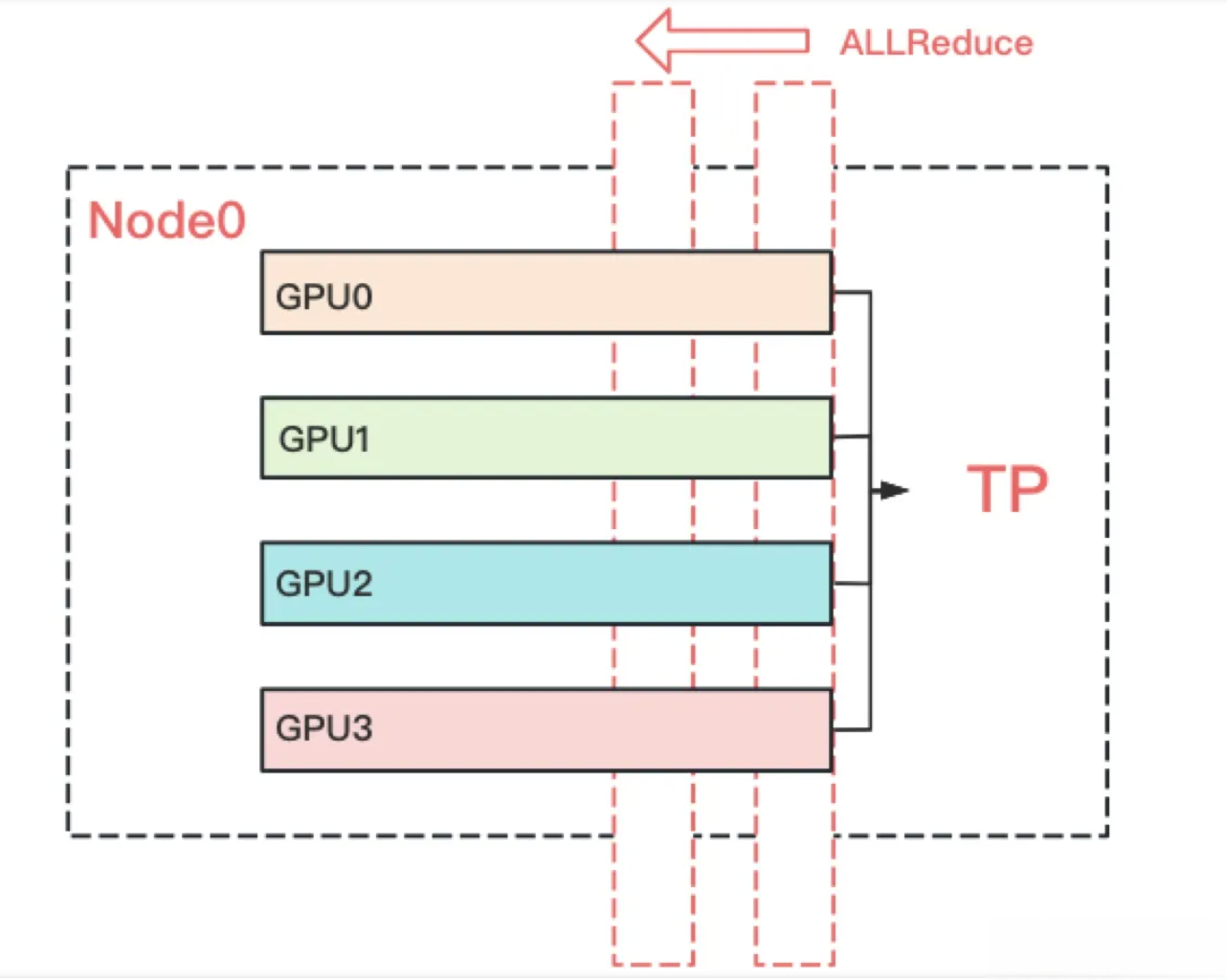
- 我们知道TP在从上一层往下一层做backward的过程中, 所有GPU间需要做一次AllReduce的, 例如下图:
- 而对DP来说, 本层算完梯度以后, 就正常把本层的梯度发出去, 和属于一个DP组的GPU做AllReduce, 同时继续往下一层做backward. 下一层也是同理. 也就是说, 在DP组中, 下一层不依赖上一层的梯度聚合结果. 因此在DP组中对带宽的要求就没那么高了, 所以可以放到机器间做DP, 例如下图: